Delaunay Triangulations Pedagogical Aid
by Shih-Ting Huang
In this project, I created an interactive pedagogical aid of Delaunay Triangulations. The visualization shows how the incremental method works on a set of random points.
Interactive demo page.
Background information and approach
- Delaunay Triangulations
Delaunay triangulations (right figure) maximize the minimum angle of all the angles of the triangles in the triangulation, and tend to avoid sliver triangles (left figure).
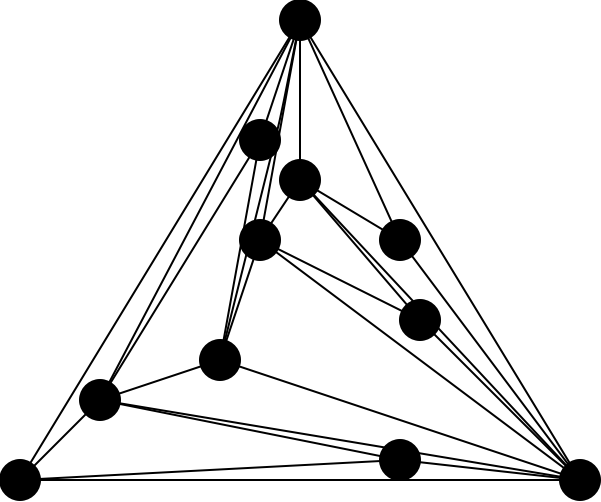 →
→
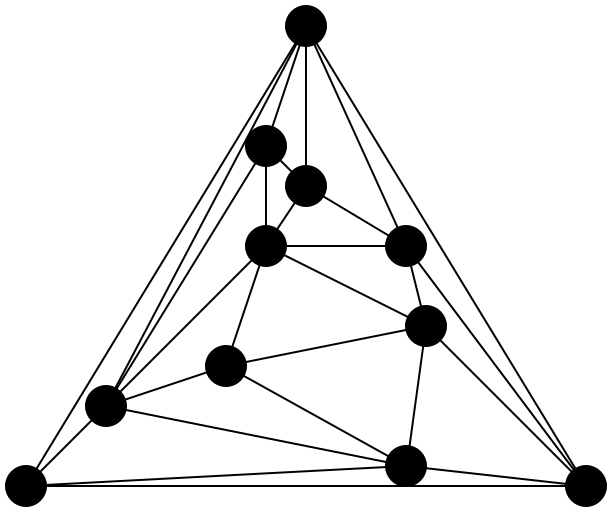
- Incremental Method
The algorithm is randomized incremental, so it adds the points in random order and it maintains a Delaunay triangulation of the current point set. In order to maintain legal Delaunay triangulation, it will perform the edge-flipping operation when triangulation fails to satisfy the empty circle property.
For example, the figure below shows that the edge (B, C) is illegal since the point D is located in the circle formed by triangle ABC. In this situation, the algorithm will filp the edge (B, C) into edge (A, D).
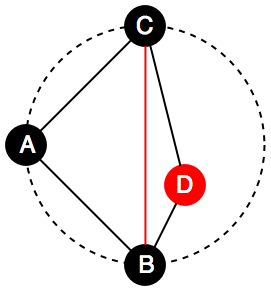 →
→
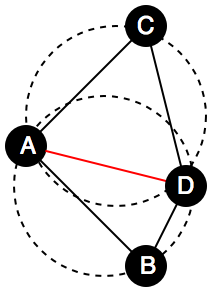
Pseudo-code
Input: a set P of n points in the plane.
Output: a Delaunay triangulation of P.
DelaunayTriangulation(P) {
Create a helper triangle contains all points.
for every point p in P {
Find the triangle abc contains p
Push edges (p, a), (p, b), (p, c) into the triangulation
SwapTest(p, a, b)
SwapTest(p, b, c)
SwapTest(p, c, a)
}
Delete all edges connected to helper points from the triangulation
return the triangulation
}
SwapTest(p, a, b) {
if (ab is an edge of helper triangle) return;
find the opposite vertex d, share same edge ab with p
if (d in the circle formed by p, a, b) {
Delete edge (a, b), and push edge(p, d) into the triangulation
SwapTest(p, a, d)
SwapTest(p, d, b)
}
Features of the Implementation
- Users can enter numbers of points on the demo page.
- The status of the algorithm is shown in top left corner of the canvas.
- The interactive demo can perform automatically or manually step by step.
- The speed of the algorithm is tunable.
- The demo page provides two background colors, black and white, to meet users' preferences.
- After Delaunay Triangulation is finished, users can click on each triangle to check the empty circle property.
References
- Computational Geometry - Algorithms and Applications (textbook)
- Delaunay Triangulation (Wikipedia)
- p5.js (Javascript library)
 →
→

 →
→
